Рассмотрим решение задачи 3 ГИА 2013 по информатике
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и F. Передвигаться можно только по дорогам, указанным в таблице.
1) 9 2) 11 3) 13 4) 15
Решение
Для удобства отобразим табличные данные в виде графа
Теперь переберем все возможные пути из A в F:
A-B-C-E-F = 3+3+2+7 = 15
A-B-C-D-F = 3+3+5+3 = 14
A-C-E-F = 5+2+7 = 14
A-C-D-F = 5+5+3 = 13
ну и A-F = 15
Как видно, кратчайший вариант A-C-D-F = 13км. Правильный ответ 3.
Чтобы не запутаться, рекомендуется перебирать пункты в алфавитном порядке.
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и B (при условии, что передвигаться можно только по построенным дорогам).
1) 11 2) 12 3) 13 4) 14
Решение:
Преобразуем таблицу в граф для удобства.
Осталось перебрать все маршруты из A в B и посмотреть их длину:
A-C-D-B = 8+1+4 = 13
A-C-E-B = 8+3+1 = 12
A-D-B = 10+4 = 14
A-D-C-E-B = 10+1+3+1 = 15
Как видим, минимальный по длине маршрут A-C-E-B, который составляет 12 километров. Правильный ответ 2.
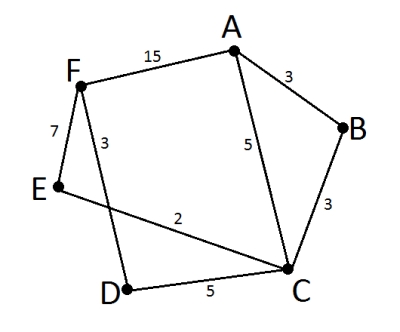
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | F | |
| A | 3 | 5 | 15 | |||
| B | 3 | 3 | ||||
| C | 5 | 3 | 5 | 2 | ||
| D | 5 | 3 | ||||
| E | 2 | 7 | ||||
| F | 15 | 3 | 7 |
1) 9 2) 11 3) 13 4) 15
Решение
Для удобства отобразим табличные данные в виде графа
Решение задачи 2 ГИА по информатике
A-B-C-E-F = 3+3+2+7 = 15
A-B-C-D-F = 3+3+5+3 = 14
A-C-E-F = 5+2+7 = 14
A-C-D-F = 5+5+3 = 13
ну и A-F = 15
Как видно, кратчайший вариант A-C-D-F = 13км. Правильный ответ 3.
Чтобы не запутаться, рекомендуется перебирать пункты в алфавитном порядке.
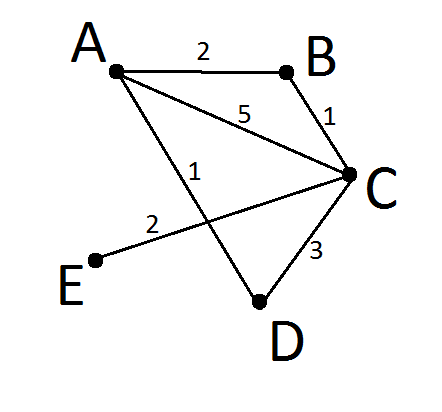
Для более качественной подготовки к ГИА по информатике рассмотрим решение задачи 3 ГИА 2014 по информатике (демоверсия ФИПИ 2014)
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | |
| A | 2 | 5 | 1 | ||
| B | 2 | 1 | |||
| C | 5 | 1 | 3 | 2 | |
| D | 1 | 3 | |||
| E | 2 |
Определите длину кратчайшего пути между
пунктами A и Е. Передвигаться можно только по дорогам, протяжённость
которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Решение:
Для удобства предлагаю поступить так же,
как и при решении задачи ГИА 2013 года и отобразить таблицу в виде
графа. Для этого на листе расставляем точки — населенные пункты. В
соответствии с таблицей соединяем их и подписываем расстояния.
Задача 3 ГИА 2014 по информатике
Осталось рассмотреть все возможные маршруты
из A в E и найти кратчайший из них. При этом обращаем внимание на то,
что в пункт E мы можем попасть только из пункта C.
A-B-C-E = 2+1+2 = 5
A-C-E = 5+2 = 7
A-D-C-E = 1+3+2 = 6
Как видим, минимальное расстояние — 5 километров (маршрут A-B-C-E). Правильный ответ 2.
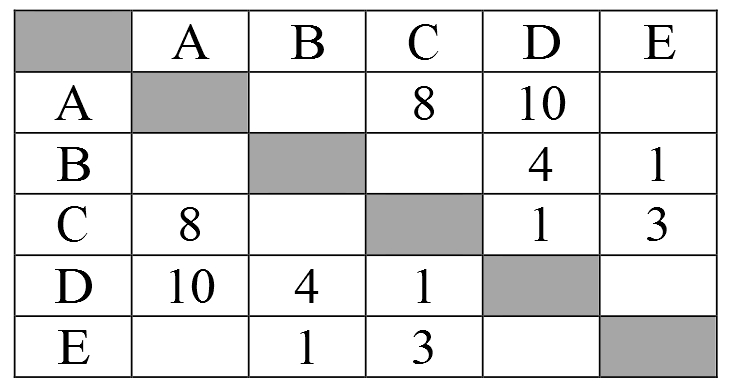
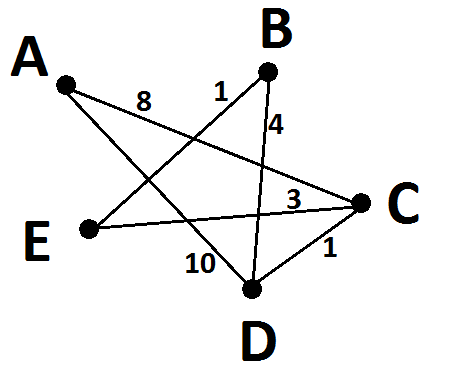
Рассмотрим решение задачи из диагностической работы ГИА по информатике 19 декабря 2013 годаМежду населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
1) 11 2) 12 3) 13 4) 14
Решение:
Преобразуем таблицу в граф для удобства.
граф к задаче 3
A-C-D-B = 8+1+4 = 13
A-C-E-B = 8+3+1 = 12
A-D-B = 10+4 = 14
A-D-C-E-B = 10+1+3+1 = 15
Как видим, минимальный по длине маршрут A-C-E-B, который составляет 12 километров. Правильный ответ 2.
Комментариев нет:
Отправить комментарий