Рассмотрим решение задачи 14. В качестве примера такой задачи возьмем задачу ГИА по информатике 2014 года по материалам ФИПИ.
У исполнителя Делитель две команды, которым присвоены номера:
(Например, 12112 – это алгоритм:
раздели на 2
вычти 1
раздели на 2
раздели на 2
вычти 1,
который преобразует число 42 в число 4).
Если таких алгоритмов более одного, то запишите любой из них.
Первое, что приходит на ум воспользоваться методом перебора всех вариантов. Но в этом случае есть вероятность запутаться, так как количество вариантов довольно большое. Поэтому, предлагаю графический метод решения.
Итак, запишем исходное число 65 по центру листа:
 По условию у исполнителя всего 2 команды — раздели на 2 и вычти 1. В
итоге после выполнения первой команды (из максимально возможных пяти) мы
можем получить два числа:
По условию у исполнителя всего 2 команды — раздели на 2 и вычти 1. В
итоге после выполнения первой команды (из максимально возможных пяти) мы
можем получить два числа:
65 /2 = 32,5
65 — 1 = 64
Но так как в условии указано, что Исполнитель работает только с натуральными числами, то число 32,5 мы сразу отбросим — оно не натуральное. Значит у нас получается такая картина:
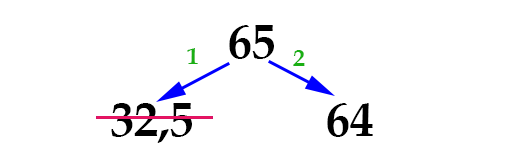
На втором шаге мы будем выполнять команды уже над числом 64. Получим такую картину:
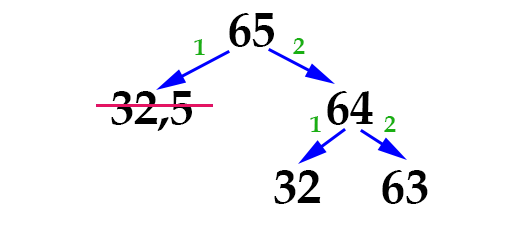 Продолжаем. На третьем шаге команды необходимо произвести уже с двумя полученными числами — 32 и 63:
Продолжаем. На третьем шаге команды необходимо произвести уже с двумя полученными числами — 32 и 63:
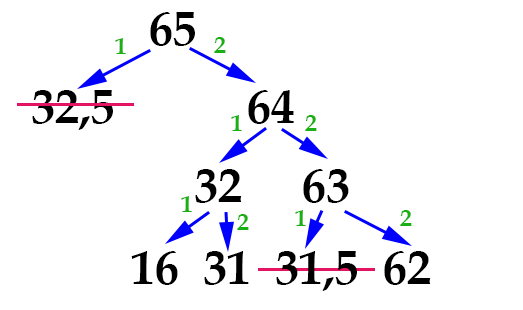 Здесь мы видим, что число 31,5 опять не удовлетворяет требованию натуральности. Продолжаем. Осталось немного
Здесь мы видим, что число 31,5 опять не удовлетворяет требованию натуральности. Продолжаем. Осталось немного  Итак, четвертый шаг:
Итак, четвертый шаг:
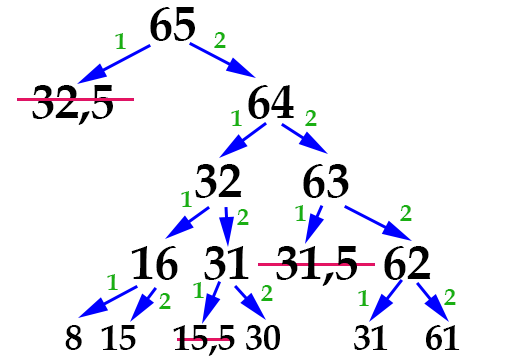 Число 15,5 мы сразу отбрасываем. Остался последний шаг! Можно опять отразить его графически:
Число 15,5 мы сразу отбрасываем. Остался последний шаг! Можно опять отразить его графически:
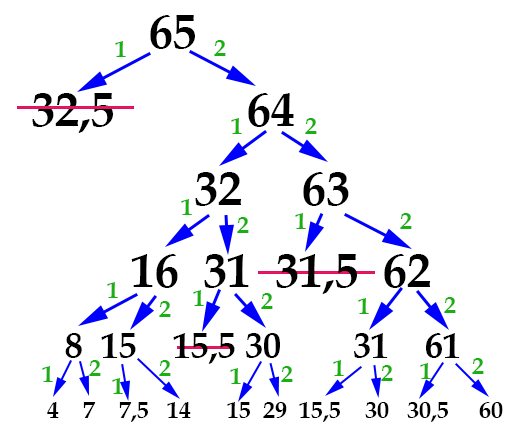 А можно просто посчитать в уме. Мы видим, что нужное число 4
получено. В ответе нам нужно указать последовательность команд. Ее мы
легко найдем, пройдя по стрелочкам от исходного числа 65 к полученному
4:
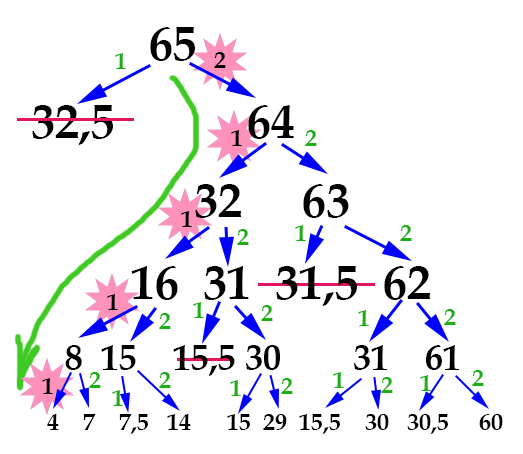
А можно просто посчитать в уме. Мы видим, что нужное число 4
получено. В ответе нам нужно указать последовательность команд. Ее мы
легко найдем, пройдя по стрелочкам от исходного числа 65 к полученному
4:
У исполнителя Делитель две команды, которым присвоены номера:
- раздели на 2
- вычти 1
(Например, 12112 – это алгоритм:
раздели на 2
вычти 1
раздели на 2
раздели на 2
вычти 1,
который преобразует число 42 в число 4).
Если таких алгоритмов более одного, то запишите любой из них.
Первое, что приходит на ум воспользоваться методом перебора всех вариантов. Но в этом случае есть вероятность запутаться, так как количество вариантов довольно большое. Поэтому, предлагаю графический метод решения.
Итак, запишем исходное число 65 по центру листа:

Решение задач типа 14 ГИА по информатике
65 /2 = 32,5
65 — 1 = 64
Но так как в условии указано, что Исполнитель работает только с натуральными числами, то число 32,5 мы сразу отбросим — оно не натуральное. Значит у нас получается такая картина:

Шаг 1
Здесь над стрелочками указаны номера команд. Левая ветвь зачеркнута —
число 32,5 натуральным не является. Это существенно облегчает нам
дальнейшее решение. Значит рассмотрим только правую ветвь.На втором шаге мы будем выполнять команды уже над числом 64. Получим такую картину:

Шаг 2

Шаг 3

Шаг 4

Шаг 5
2 1 1 1 1

Решение
Это и есть правильный ответ.
Комментариев нет:
Отправить комментарий